放物線座標と楕円座標

　円筒座標 $\left(\rho,\,\varphi,\,z\right)$ から放物座標 $\left(\xi,\,\eta,\,\varphi\right)$ への変換は、公式 \begin{eqnarray} z & = & \dfrac{1}{2}\left(\xi-\eta\right)\label{eq:1}\\ \rho & = & \sqrt{\xi\eta}\label{eq:2} \end{eqnarray} でおこなわれる（図1(a)）。座標 $\xi$ と $\eta$ は \begin{equation} 0\leq\xi,\,\eta<\infty\label{eq:3} \end{equation} の値をとる。

　$\eta=\mathrm{const}$ の面は、式(\ref{eq:2})より $\xi=\dfrac{\rho^{2}}{\eta}$ を式(\ref{eq:1})へ代入して \begin{equation} z=\dfrac{1}{2}\left(\dfrac{\rho^{2}}{\eta}-\eta\right)\label{eq:4} \end{equation} となり、$z$ と $\rho$ の関係は放物線で表わされ、式(\ref{eq:4})は $z$ 軸を対称軸とする下に凸の回転放物面となる（図1(b)）。同様に、$\xi=\mathrm{const}$ の面は、$\eta=\dfrac{\rho^{2}}{\xi}$ であるので \begin{equation} z=\dfrac{1}{2}\left(\xi-\dfrac{\rho^{2}}{\xi}\right)\label{eq:5} \end{equation} となり、上に凸の回転放物面を与える。これらの放物線の焦点は $z$ 軸上の $z=0$ である。

図1　(a) 円筒座標、(b) 回転放物面

　$\xi=\mathrm{const}$ と $\eta=\mathrm{const}$ の曲面からなる $\varphi=\mathrm{const}$ の断面は、図2に示すように放物線座標となっている。また、これらの曲線はたがいに直交していることが以下のようにわかる。

　交点での曲線の傾きを求めると、$\xi=\mathrm{const}$ に対しては \[ \dfrac{dz_{\xi}}{d\rho}=-\dfrac{\rho}{\xi} \] $\eta=\mathrm{const}$ に対しては \[ \dfrac{dz_{\eta}}{d\rho}=\dfrac{\rho}{\eta} \] したがって、傾きの積が \[ \dfrac{dz_{\xi}}{d\rho}\cdot\dfrac{dz_{\eta}}{d\rho}=-\dfrac{\rho}{\xi\eta}=-1 \] となることから直交していることが確かめられる。

図2　放物線座標

　式(\ref{eq:1})および(\ref{eq:2})の関係は、半径（図1(a)） \begin{equation} r=\sqrt{z^{2}+\rho^{2}}=\sqrt{\dfrac{1}{4}\left(\xi-\eta\right)^{2}+\xi\eta}=\dfrac{1}{2}\left(\xi+\eta\right)\label{eq:6} \end{equation} を導入して他の形に書くことができる。式(\ref{eq:1})および(\ref{eq:6})より \begin{equation} \xi=r+z,\quad\eta=r-z\label{eq:7} \end{equation} となる。

　円筒座標 $\left(\rho,\,\varphi,\,z\right)$ から楕円座標 $\left(\xi,\,\eta,\,\varphi\right)$ への変換は、公式 \begin{eqnarray} z & = & \sigma\xi\eta\label{eq:8}\\ \rho & = & \sigma\sqrt{\left(\xi^{2}-1\right)\left(1-\eta^{2}\right)}\label{eq:9} \end{eqnarray} でおこなわれる。ここで定数 $\sigma$ は変換のパラメーターである。座標 $\xi$ と $\eta$ は \begin{equation} 1<\xi<\infty,\quad-1<\eta<+1\label{eq:10} \end{equation} の値をとる。

　$\xi=\mathrm{const}$ の面は、$\eta=\dfrac{z}{\sigma\xi}$ であるので \[ \rho^{2}=\sigma^{2}\left(\xi^{2}-1\right)\left(1-\dfrac{z^{2}}{\sigma^{2}\xi^{2}}\right) \] すなわち \begin{equation} \dfrac{z^{2}}{\left(\sigma\xi\right)^{2}}+\dfrac{\rho^{2}}{\left(\sigma\sqrt{\xi^{2}-1}\right)^{2}}=1\label{eq:11} \end{equation} となる。$\sigma\xi>\sigma\sqrt{\xi^{2}-1}$ であるので、式(\ref{eq:11})は $z$ 軸を長半径とする回転楕円面（ $z$ 軸を対称軸とする）である（図3(b)）。この楕円面の焦点は、$z$ 軸上の点 $z=\pm\sigma$ である。同様に、$\eta=\mathrm{const}$ の面は、$\xi=\dfrac{z}{\sigma\eta}$ であるので \[ \rho^{2}=\sigma^{2}\left(\dfrac{z^{2}}{\sigma^{2}\eta^{2}}-1\right)\left(1-\eta^{2}\right) \] すなわち \begin{equation} \dfrac{z^{2}}{\left(\sigma\eta\right)^{2}}-\dfrac{\rho^{2}}{\left(\sigma\sqrt{1-\eta^{2}}\right)^{2}}=1\label{eq:12} \end{equation} となり、$z$ 軸を対称軸とする回転双曲線面（図3(b)）となる。この双曲線面の焦点も同じく、$z$ 軸上の点 $z=\pm\sigma$ である。

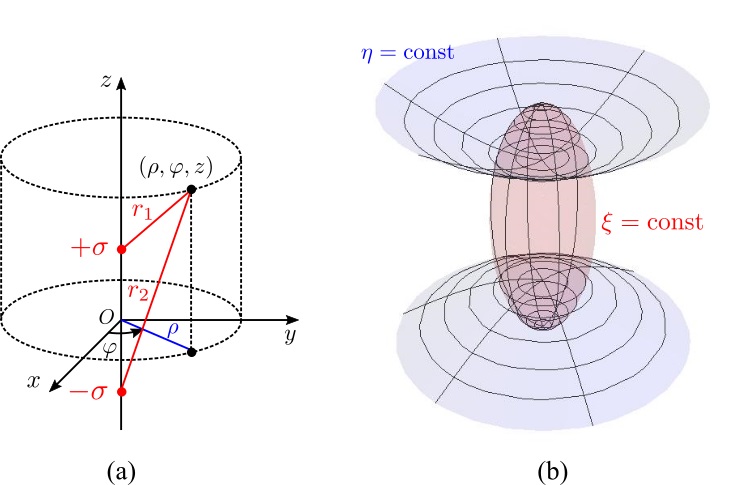
図3　(a) 円筒座標、(b) 回転楕円面と回転双曲線面

図4　楕円座標

　$\xi=\mathrm{const}$ と $\eta=\mathrm{const}$ の曲面からなる $\varphi=\mathrm{const}$ の断面は、図4に示すように楕円座標となっている。また、これらの曲線はたがいに直交していることが以下のようにわかる。交点での曲線の傾きを求めると、$\xi=\mathrm{const}$ に対しては \[ \dfrac{2z}{\left(\sigma\xi\right)^{2}}\dfrac{dz_{\xi}}{d\rho}+\dfrac{2\rho}{\left(\sigma\sqrt{\xi^{2}-1}\right)^{2}}=0 \] より \[ \dfrac{dz_{\xi}}{d\rho}=-\dfrac{\left(\sigma\xi\right)^{2}}{\left(\sigma\sqrt{\xi^{2}-1}\right)^{2}}\dfrac{\rho}{z} \] $\eta=\mathrm{const}$ に対しては \[ \dfrac{2z}{\left(\sigma\eta\right)^{2}}\dfrac{dz_{\eta}}{d\rho}-\dfrac{2\rho}{\left(\sigma\sqrt{1-\eta^{2}}\right)^{2}}=0 \] より \[ \dfrac{dz_{\eta}}{d\rho}=\dfrac{\left(\sigma\eta\right)^{2}}{\left(\sigma\sqrt{1-\eta^{2}}\right)^{2}}\dfrac{\rho}{z} \] したがって、傾きの積は \[ \dfrac{dz_{\xi}}{d\rho}\cdot\dfrac{dz_{\eta}}{d\rho}=-\dfrac{\xi^{2}\eta^{2}}{\left(\xi^{2}-1\right)\left(1-\eta^{2}\right)}\dfrac{\rho^{2}}{z^{2}}=-1 \] となり、直交していることが確かめられる。

　座標の値 $z=\sigma,\,z=-\sigma$ の $z$ 軸上の2点 $A_{1},\,A_{2}$ までの距離 \begin{equation} r_{1}=\sqrt{\left(z-\sigma\right)^{2}+\rho^{2}},\quad r_{2}=\sqrt{\left(z+\sigma\right)^{2}+\rho^{2}}\label{eq:13} \end{equation} を導入すると（図3(a)）、幾何学的にずっと見やすい関係が得られる。

　式(\ref{eq:8})および(\ref{eq:9})を式(\ref{eq:13})へ代入して \begin{eqnarray*} r_{1} & = & \sigma\sqrt{\left(\xi\eta-1\right)^{2}+\left(\xi^{2}-1\right)\left(1-\eta^{2}\right)}\\ & = & \sigma\sqrt{\xi^{2}\eta^{2}-2\xi\eta+1+\xi^{2}-\xi^{2}\eta^{2}-1+\eta^{2}}\\ & = & \sigma\sqrt{\left(\xi-\eta\right)^{2}} \end{eqnarray*} ここで式(\ref{eq:10})より、$\xi>\eta$ であるので \begin{equation} r_{1}=\sigma\left(\xi-\eta\right)\label{eq:14} \end{equation} となる。同様に \begin{eqnarray} r_{2} & = & \sigma\sqrt{\left(\xi\eta+1\right)^{2}+\left(\xi^{2}-1\right)\left(1-\eta^{2}\right)}\nonumber \\ & = & \sigma\sqrt{\xi^{2}\eta^{2}+2\xi\eta+1+\xi^{2}-\xi^{2}\eta^{2}-1+\eta^{2}}\nonumber \\ & = & \sigma\left(\xi+\eta\right)\label{eq:15} \end{eqnarray} となる。これらより \begin{equation} \xi=\dfrac{\sigma}{2}\left(r_{1}+r_{2}\right),\quad\eta=\dfrac{\sigma}{2}\left(r_{2}-r_{1}\right)\label{eq:16} \end{equation} となる。

　放物線、楕円、双曲線の焦点についてまとめておく。

　定直線（準線）からの距離と、定点（焦点）からの距離が等しいような点の軌跡 $C$ を考える。焦点を $F\left(0,\,f\right)$、準線を $y=a$（ただし、$f>a$ とする）とし、軌跡 $C$ 上の点を $P\left(x,\,y\right)$ とする。図5(a)に示すように、点 $P$ から準線におろした垂線の足を点 $H$ とすれば、軌跡 $C$ 上の点に対しては \[ |PF|=|PH| \] が成り立つ。したがって \[ \sqrt{x^{2}+\left(f-y\right)^{2}}=|y-a| \] 両辺2乗して整理すれば \begin{eqnarray} x^{2}+\left(f-y\right)^{2} & = & \left(y-a\right)^{2}\nonumber \\ x^{2}+f^{2}-2fy+y^{2} & = & y^{2}-2ay+a^{2}\nonumber \\ -2\left(f-a\right)y & = & -x^{2}-\left(f^{2}-a^{2}\right)\nonumber \\ y & = & \dfrac{x^{2}}{2\left(f-a\right)}+\dfrac{f+a}{2}\label{eq:17} \end{eqnarray} となり、軌跡 $C$ は放物線を描くことがわかる。

　式(\ref{eq:17})と式(\ref{eq:4}) \[ z=\dfrac{1}{2}\left(\dfrac{\rho^{2}}{\eta}-\eta\right) \] を比較すれば \[ f-a=\eta,\quad f+a=-\eta \] であることから \[ f=0,\quad a=-\eta \] となる。このことから式(\ref{eq:4})の放物線はの焦点は $\left(0,\,0\right)$、準線は $y=-\eta$ であることがわかる。

　同様に、式(\ref{eq:17})と式(\ref{eq:5}) \[ z=\dfrac{1}{2}\left(\xi-\dfrac{\rho^{2}}{\xi}\right) \] を比較すれば \[ f-a=-\xi,\quad f+a=\xi \] であることから \[ f=0,\quad a=\xi \] となる。このことから式(\ref{eq:5})の放物線の焦点は $\left(0,\,0\right)$、準線は $y=\xi$ であることがわかる。

　2定点（焦点）からの距離の和が一定とような点の軌跡$C$を考える。2定点 $F,\,F'$ を $x$ 軸上にとり、$FF'$ の中点を座標原点とすれば、2定点の位置は $F\left(f,\,0\right),\,F'\left(-f,\,0\right)$ と表わされる（図5(b)）。軌跡 $C$ 上の点を $P\left(x,\,y\right)$ とすれば \begin{equation} |PF|=\sqrt{\left(x-f\right)^{2}+y^{2}},\quad|PF'|=\sqrt{\left(x+f\right)^{2}+y^{2}}\label{eq:18} \end{equation} となり、軌跡 $C$ 上の点に対しては \begin{equation} |PF|+|PF'|=\mathrm{const}=2a\quad(a>f)\label{eq:19} \end{equation} が成り立つ。ここで $y=0$ となる点 $P$ を考えれば、$a>f$ となることがわかる。

　式(\ref{eq:18})を式(\ref{eq:19})へ代入して \[ \sqrt{\left(x-f\right)^{2}+y^{2}}+\sqrt{\left(x+f\right)^{2}+y^{2}}=2a \] 上式の左辺第2項を右辺に移し、両辺を2乗すれば \begin{eqnarray*} \left(x-f\right)^{2}+y^{2} & = & \left(x+f\right)^{2}+y^{2}-4a\sqrt{\left(x+f\right)^{2}+y^{2}}+4a^{2}\\ -fx & = & fx+2a^{2}-2a\sqrt{\left(x+f\right)^{2}+y^{2}} \end{eqnarray*} より \[ a\sqrt{\left(x+f\right)^{2}+y^{2}}=fx+a^{2} \] さらに両辺を2乗して整理すると \begin{eqnarray} a^{2}\left(\left(x+f\right)^{2}+y^{2}\right) & = & \left(fx+a^{2}\right)^{2}\nonumber \\ a^{2}\left(x^{2}+2fx+f^{2}+y^{2}\right) & = & f^{2}x^{2}+2a^{2}fx+a^{4}\nonumber \\ a^{2}x^{2}+a^{2}\left(f^{2}+y^{2}\right) & = & f^{2}x^{2}+a^{4}\nonumber \\ \left(a^{2}-f^{2}\right)x^{2}+a^{2}y^{2} & = & a^{2}\left(a^{2}-f^{2}\right)\nonumber \\ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{a^{2}-f^{2}} & = & 1\label{eq:20} \end{eqnarray} となり、軌跡 $C$ は楕円を描くことがわかる。

　式(\ref{eq:20})と式(\ref{eq:11}) \[ \dfrac{z^{2}}{\left(\sigma\xi\right)^{2}}+\dfrac{\rho^{2}}{\left(\sigma\sqrt{\xi^{2}-1}\right)^{2}}=1 \] を比較すれば \[ a=\sigma\xi,\quad a^{2}-f^{2}=\sigma^{2}\left(\xi^{2}-1\right) \] となるので \[ f^{2}=\left(\sigma\xi\right)^{2}-\sigma^{2}\left(\xi^{2}-1\right)=\sigma^{2} \] より \[ f=\pm\sigma \] となる。このことから式(\ref{eq:11})の楕円の焦点は $z$ 軸上の $z=\pm\sigma$ にあり、その長半径が $\sigma\xi$ であることがわかる。

　2定点（焦点）からの距離の差が一定とような点の軌跡 $C$ を考える。2定点 $F,\,F'$ を $x$ 軸上にとり、$FF'$ の中点を座標原点とすれば、2定点の位置は $F\left(f,\,0\right),\,F'\left(-f,\,0\right)$ と表わされる（図5(c)）。軌跡 $C$ 上の点を $P\left(x,\,y\right)$ とすれば \begin{equation} |PF|=\sqrt{\left(x-f\right)^{2}+y^{2}},\quad|PF'|=\sqrt{\left(x+f\right)^{2}+y^{2}}\label{eq:21} \end{equation} となり、軌跡 $C$ 上の点に対しては \begin{equation} |PF'|-|PF|=\mathrm{const}=2a\quad(a< f)\label{eq:22} \end{equation} が成り立つ。ここで $y=0$ となる点 $P$ を考えれば、$a< f$ となることがわかる。

　式(\ref{eq:21})を式(\ref{eq:22})へ代入して \[ \sqrt{\left(x+f\right)^{2}+y^{2}}-\sqrt{\left(x-f\right)^{2}+y^{2}}=2a \] 上式の左辺第2項を右辺に移し、両辺を2乗すれば \begin{eqnarray*} \left(x+f\right)^{2}+y^{2} & = & \left(x-f\right)^{2}+y^{2}+4a\sqrt{\left(x-f\right)^{2}+y^{2}}+4a^{2}\\ fx & = & -fx+2a^{2}+2a\sqrt{\left(x-f\right)^{2}+y^{2}} \end{eqnarray*} より \[ a\sqrt{\left(x-f\right)^{2}+y^{2}}=fx-a^{2} \] さらに両辺を2乗して整理する \begin{eqnarray*} a^{2}\left(\left(x-f\right)^{2}+y^{2}\right) & = & \left(fx-a^{2}\right)^{2}\\ a^{2}\left(x^{2}-2fx+f^{2}+y^{2}\right) & = & f^{2}x^{2}-2a^{2}fx+a^{4}\\ a^{2}x^{2}+a^{2}\left(f^{2}+y^{2}\right) & = & f^{2}x^{2}+a^{4}\\ \left(a^{2}-f^{2}\right)x^{2}+a^{2}y^{2} & = & a^{2}\left(a^{2}-f^{2}\right)\\ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{a^{2}-f^{2}} & = & 1 \end{eqnarray*} ここで $a< f$ であることに注意すれば \begin{equation} \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{f^{2}-a^{2}}=1\label{eq:23} \end{equation} となり、軌跡 $C$ は双曲線を描くことがわかる。

　式(\ref{eq:23})と式(\ref{eq:12}) \[ \dfrac{z^{2}}{\left(\sigma\eta\right)^{2}}-\dfrac{\rho^{2}}{\left(\sigma\sqrt{1-\eta^{2}}\right)^{2}}=1 \] を比較すれば \[ a=\sigma\eta,\quad f^{2}-a^{2}=\sigma^{2}\left(1-\eta^{2}\right) \] となるので \[ f^{2}=\left(\sigma\eta\right)^{2}+\sigma^{2}\left(1-\eta^{2}\right)=\sigma^{2} \] より \[ f=\pm\sigma \] となる。このことから式(\ref{eq:12})の双曲線の焦点も $z$ 軸上の $z=\pm\sigma$ にあることがわかる。

図5　(a) 放物線、(b) 楕円、(c) 双曲線