多価関数とリーマン面

　複素関数 $w=f(z)$ において、$z$ 平面上の 1 つの点が $w$ 平面上の 2 つまたはそれより多くの点に対応するときには、一般に $w=f(z)$ を $z$ の多価関数という。

　簡単な関数 \begin{equation} w=z^{1/2}\label{eq:1} \end{equation} を考える。$z=re^{i\theta}=re^{i(\theta+2n\pi)}\;(n:0 \text{または整数})$とおけば \[ w=\sqrt{r}e^{i\theta/2+in\pi}=(-1)^{n}\sqrt{r}e^{i\theta/2} \] ゆえに \begin{eqnarray*} w_{1} & = & \sqrt{r}e^{i\theta/2}\\ w_{2} & = & \sqrt{r}e^{i\theta/2+i\pi} \end{eqnarray*} とおけば、式(\ref{eq:1})によって与えられた $w$ は 2 つの異なる値 $w_{1}$ および $w_{2}$ を表す。そうして $w_{2}=-w_{1}$ である（同じ $z$ の値に対して、異なる 2 つの値が対応している）。

　$z$ が $z$ 平面上のある曲線によってその値を変えれば、これに応じて $w_{1}$ および $w_{2}$ は別々に $w$ 平面上の曲線に沿ってその値を変える。例えば、図1において、$|z|=\mathrm{const}$ として点 $z$ を原点を中心とする円周上で動かし、$\arg z$ を 0 から $2\pi$ まで変えたとき、その $w$ 平面上の写像はどのように変わるかを考える。$z$ が $A$ から出発して原点の周りを一周する間に、$w_{1}$ は $w$ 平面上を $A'$ から $B'$ を経て $A''$ に至る半円周を描き、$w_{2}$ は $A''$ から出発して $B''$ を経て $A'$ に至る半円周を描く。このことは、$|z|=\mathrm{const}$ でなくても、$z$ が原点を囲む任意の曲線（図1の破線）に沿って動かすときでも同様である。このように $z$ を動かしたときの $w_{1}$ および $w_{2}$ の変域は別々に分かれている。

図1 (a) $z=x+iy$ 平面、(b) $w=u+iv$ 平面

　もし $z$ 平面上で原点から $x$ 軸の正の方向に沿って垣を作り、その平面上の曲線がこれを超すことができないように制限を付けたとすれば、$z$ 平面上の任意の曲線に対応する $w$ 平面上の写像は、その $u$ 軸によって上下に分かれた別々の変域になる（ $w_{1},\,w_{2}$ の変域はそれぞれ $u$ 軸の上側（上半面）、$u$ 軸の下側（下半面）となる）。これらの変域を関数 $w=z^{1/2}$ の岐帯と名づけ、その境界に対応する $z$ 平面上の垣を切断という。

　切断を作らない $z$ 平面上で、$z$ が $P$ から出発して原点を 2 回（あるいは $2n$ 回）まわってもとの $P$ に戻る移動に対しては、$w$ は $Q$ から出発して原点を 1 周（あるいは $n$ 周）してもとの $Q$ に戻る（図2）。

図2 (a) $z=x+iy$ 平面、(b) $w=u+iv$ 平面

　この例で示したように、$z$ 平面上のある点を少なくとも $n$ 回まわることによって、$w$ 平面上のこれに対応する値がもとに復帰するような性質を持つ点を $(n-1)$ 位の代数的分岐点という。

　$z=\infty$ に対しては、$z=1/\zeta$ とおいて $\zeta=0$ の周りを調べる。 \begin{equation} w=\zeta^{-1/2}\label{eq:2} \end{equation} となるので$\zeta=\alpha e^{i\theta}$とおくと \[ w=\dfrac{1}{\sqrt{\alpha}}e^{-i\theta/2-in\pi}=(-1)^{n}\dfrac{1}{\sqrt{\alpha}}e^{-i\theta/2} \] ゆえに \begin{eqnarray*} w_{1} & = & \dfrac{1}{\sqrt{\alpha}}e^{-i\theta/2}\\ w_{2} & = & \dfrac{1}{\sqrt{\alpha}}e^{-i\theta/2-i\pi}=-w_{1} \end{eqnarray*} とおくことができ、$z=0$ のまわり同様の振る舞いをするので、$z=\infty\,(\zeta=0)$ もまた（1位の）分岐点となっている（式(\ref{eq:2})が $\zeta$ の非整数のべきであることからも明らかである）。

　$P$ から出発して分岐点（ $z=0$ ）を内部に含まない経路を通ってもとの $P$ に戻る $z$ の変化に対しては、$w$ の方はこれに対応して、$w_{1}$ は $Q$ から出発して元に戻る経路に変わり、$w_{2}$ は原点に対してこれと対称の経路に沿って変わる（図3）。

図3 (a) $z=x+iy$ 平面、(b) $w=u+iv$ 平面

　次に、対数関数 \begin{equation} w=\ln\left(z-a\right)\label{eq:3} \end{equation} を考える。$z-a=re^{i\theta}$とおけば \[ w=\ln r+i\left(\theta+2n\pi\right)\;(n:0\text{ま\text{た\text{は\text{整\text{数}}}}}) \] ゆえに、$w=u+iv$ として \[ u=\ln r=\ln|z-a|,\qquad v=\theta+2n\pi \] したがって $z$ 平面上において点 $a$ から任意の方向に直線（図4：赤実線）を引くとき、すなわち $\theta=\mathrm{const}$ として $r$ だけ変化させるときには、その $w$ 平面上の写像は $u$ 軸に平行で $2\pi$ ずつの隔たりを持つ多くの平行線になる（図4：赤実線）。

図4 (a) $z=x+iy$ 平面、(b) $w=u+iv$ 平面

　もし $z$ 平面上に描いた直線（図4(a)：赤実線）に沿って切断を作って、その平面上の曲線がこれを超えさせないように制限を加えたとすれば、$z$平面上の曲線（図4(a)：青実線）は $w$ 平面上の互いに $2\pi$ ずつ隔たった平行直線（図4(b)：赤実線）間の岐帯の各部に 1 つずつ別々の写像となって現れる（図4(b)：青実線）。

　$z=a$ なる点においては関数の値は全く不定である。これはその虚数部の値がその点において全く不定であることによる。

　点 $a$ 以外の任意の点 $z_{1}=a+r_{1}e^{i\theta_{1}}$ をとればこれに対応する $w$ の値は \[ w=\ln r_{1}+i\theta_{1}+2n\pi i \] である。切断を作らない $z$ 平面において、$z$ の値を $z_{1}$ から出発して $a$ を 1 周だけ取り巻く曲線に沿って変化させ、もとの $z_{1}$ に帰らせれば、$a$ を回る方向が正であるか負であるかによって、$w$ の値は $w=\ln r_{1}+i\theta_{1}+2(n+1)\pi i$ かまたは $w=\ln r_{1}+i\theta_{1}+2(n-1)\pi i$ になる。このように、$z$ 平面上に $z$ が $a$ なる点を適当な回数だけ回る経路に沿ってその値を変化させることによって、これに対応する $w$ 平面上の点が $w$ の任意の岐帯にあるようにすることができる。しかし、$z=a$ を何回同じ方向に回っても $w$ の値は決して元の値に戻ることはない。このような場合に $z=a$ を対数的分岐点という。

　再び前節で説明した関数 \[ w=z^{1/2} \] をとって考えれば、$z$ が $\arg z$ を 0 から $2\pi$ まで変える間に、$w$ は $w_{1}$ なる形をとって $w$ 平面の上半部にその値を変える。$z$ が原点を 1 周した後、その $\arg z$ がさらに $2\pi$ から $4\pi$ まで変わるときには、$w$ は $w_{2}$ すなわち $-w_{1}$ なる型を取って $w$ 平面の下半部にその値を変える。ゆえに 1 枚の $z$ 平面の代わりに 2 枚の $z$ 平面 $S_{1}$ および $S_{2}$ を用い、始めの $\arg z$ が 0 から $2\pi$ まで変わることを示すのに $S_{1}$ 平面を用い、後の $2\pi$ から $4\pi$ まで変わることを示すのに $S_{2}$ 平面を用いれば、この 2 枚の $z$ 平面上の任意の 1 つの点は $w$ 平面上の 1 つの点に対応するものと考えることができる。すなわち、2 枚の $z$ 平面と 1 枚の $w$ 平面が 1 対 1 対応の関係にあると見なすことができる。

　しかしだだ 2 枚の $z$ 平面を別々にしておいたのでは、$\arg z$ を連続的に 0 から $2\pi$ を経て $4\pi$ まで変化させることは考え難い。この不便を救う策として、$S_{1}$ および $S_{2}$ の各平面をその分岐点 0 と $\infty$ とを結ぶ線、例えば正の実数軸に沿って切断を入れ、図5に示したように、切断に沿って $S_{1}$ の切り口の下端と $S_{2}$ の切り口の上端をつなげ、$S_{2}$ の下端と $S_{1}$ の上端とをつないだものとしよう。このような平面上で、例えば $S_{1}$ 上の点 $z_{1}$ から出発して原点をまわって $A$ のところで $S_{2}$ 平面に入りさらに原点を周って再び $A$ の所でもとの $S_{1}$ 平面に出て $z_{1}$ に帰るような経路を取れば、結局原点を 2 回続けてまわったことになる。すなわち $z_{1}$ から出発して再び $z_{1}$ に帰るために原点を 2 回まわるのである。このように 2 枚の $z$ 平面を適当に接続して、その上の 1 つの点と $w$ 平面上の 1 つの点とを連続的かつ 1 対 1 の関係によって結びつけ、その意味で 1 価関数の場合と同じように写像関係を表現しうるようにする平面を関数 $z^{1/2}$ のリーマン面という。

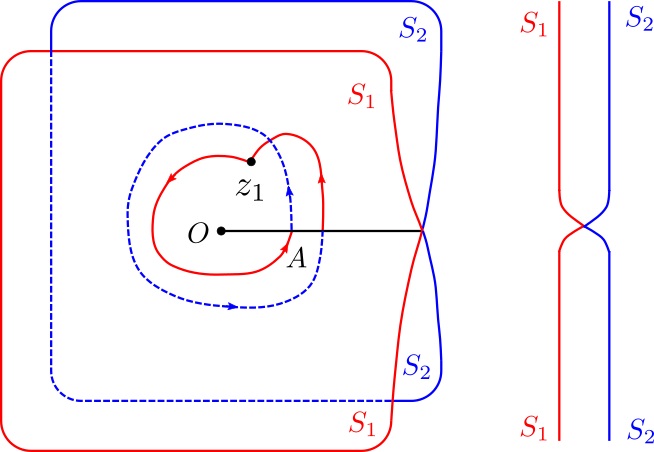
図5 関数 $z^{1/2}$ のリーマン面

　同様に関数 $(z-a)^{1/2}$ は 2 つの分岐点 $a$ と $\infty$ をもつから、$a$ と $\infty$ とを結ぶ任意の線を切断として上のように連結した平面は関数 $(z-a)^{1/2}$ のリーマン面である。もっと一般に、$z$ と $(z-a)^{1/2}$ との有理関数のリーマン面も上と同じである。特に、多価関数 $w=z^{1/n}\;(n\text{：整数)}$ に対しては、正の実数軸上に切断を入れた $n$ 枚の平面 $S_{1},\,S_{2},\,\cdots\,,S_{n}$ を考え、$S_{1}$ の下端を $S_{2}$ の上端に、$S_{2}$ の下端を $S_{3}$ の上端に、$\cdots,\,$$S_{n}$ の下端を $S_{1}$ の上端に貼りつけたリーマン面を考えればよい。

　複素関数論における正則とか極とかいう言葉は 1 枚の $z$ 平面上においての 1 価関数に関して定義されたものであるが、いま述べた方法によって、多価関数に対するリーマン面を作りこれを $z$ 平面に代用すれば、多価関数も 1 価関数と同様の有様を呈する（コーシーの積分定理が適用できる）。

　関数 \begin{equation} w=\sqrt{(z-a)(z-b)}\quad(a,\,b\in\mathbb{R})\label{eq:4} \end{equation} を例として分岐点と切断の入れ方を考える。ここで、点 $a,\,b$ 周りの極座標表示 \begin{eqnarray*} z-a & = & \alpha e^{i\theta}\\ z-b & = & \beta e^{i\varphi} \end{eqnarray*} を用いる（図6 (i)）。このとき偏角の変化 \begin{eqnarray*} \theta & \rightarrow & \theta+2n\pi\\ \varphi & \rightarrow & \varphi+2m\pi\quad(n.\,m=0,\,\pm1,\,\pm2,\,\cdots\,) \end{eqnarray*} に対して $z$ の値は同一である。これより \begin{eqnarray*} w & = & \sqrt{\alpha\beta}e^{\frac{i}{2}(\theta+\varphi+2(n+m)\pi)}\\ & = & \sqrt{\alpha\beta}e^{\frac{i}{2}(\theta+\varphi)+i(n+m)\pi}\\ & = & (-1)^{n+m}\sqrt{\alpha\beta}e^{\frac{i}{2}(\theta+\varphi)} \end{eqnarray*} ゆえに \begin{eqnarray*} w_{1} & = & \sqrt{\alpha\beta}e^{\frac{i}{2}(\theta+\varphi)}\\ w_{2} & = & \sqrt{\alpha\beta}e^{\frac{i}{2}(\theta+\varphi)+i\pi}=-w_{1} \end{eqnarray*} とおけば、式(\ref{eq:4})によって与えられた $w$ は 2 つの異なる値 $w_{1}$ および $w_{2}$ を表す。そうして $w_{2}=-w_{1}$ である（同じ $z$ の値に対して、異なる 2 つの値が対応している）。

図6 (i) 極座標、(ii) 点 $a$ を 1 周する経路、(ii) 点 $b$ を 1周する経路

　$w$ の値を $w=w_{1}$ とすると（点 $b$ を含まない）点 $a$ まわりに 1 周する経路（図6(ii)）に対する偏角の変化は \begin{eqnarray*} \theta & \rightarrow & \theta+2\pi\\ \varphi & \rightarrow & \varphi \end{eqnarray*} より \[ w=w_{1}\;\rightarrow\;w=w_{2}=-w_{1} \] となる。（点 $b$ を含まない）点 $a$ まわりに 2 周する経路に対する偏角の変化は \begin{eqnarray*} \theta & \rightarrow & \theta+2\pi\;\rightarrow\;\theta+4\pi\\ \varphi & \rightarrow & \varphi\;\rightarrow\;\varphi \end{eqnarray*} より \[ w=w_{1}\;\rightarrow\;w=w_{1} \] となり、2 周で元に戻る。

　同様に、（点 $a$ を含まない）点 $b$ まわりに 1 周する経路（図6 (iii)）に対する偏角の変化は \begin{eqnarray*} \theta & \rightarrow & \theta\\ \varphi & \rightarrow & \varphi+2\pi \end{eqnarray*} より \[ w=w_{1}\;\rightarrow\;w=w_{2}=-w_{1} \] となる。（点 $a$ を含まない）点 $b$ まわりに 2 周する経路に対する偏角の変化は \begin{eqnarray*} \theta & \rightarrow & \theta\;\rightarrow\;\theta\\ \varphi & \rightarrow & \varphi+2\pi\;\rightarrow\;\varphi+4\pi \end{eqnarray*} より \[ w=w_{1}\;\rightarrow\;w=w_{1} \] となり、2 周で元に戻る。このように点 $a$ か点 $b$ のどちらか一方のまわりに 2 周する経路によって $w$ は元の値に戻るので、点 $a$ および点 $b$ は 1 位の分岐点であることがわかる。

　一方、点 $a$ と点 $b$ の両方を内側に含む経路（図7 (i)）で 1 周すると \begin{eqnarray*} \theta & \rightarrow & \theta+2\pi\\ \varphi & \rightarrow & \varphi+2\pi \end{eqnarray*} より \[ w=w_{1}\;\rightarrow\;w=w_{1} \] と $w$ は変化しない。同様に、点 $a$ と点 $b$ の両方を内側に含まない経路（図7 (ii)）で 1 周すると \begin{eqnarray*} \theta & \rightarrow & \theta\\ \varphi & \rightarrow & \varphi \end{eqnarray*} であるので \[ w=w_{1}\;\rightarrow\;w=w_{1} \] と $w$ は変化しない。

図7 (i) 点 $a,\,b$ をともに含む経路、(ii) 点 $a,\,b$ をともに含まない経路

　無限遠点 $z=\infty$（絶対値無限大、偏角不定）に対しては、 \[ z=\dfrac{1}{\zeta}\;(\zeta\rightarrow0) \] とおいて、$\zeta=0$ について考えると \begin{eqnarray*} w & = & \sqrt{\left(\dfrac{1}{\zeta}-a\right)\left(\dfrac{1}{\zeta}-b\right)}\\ & = & \dfrac{1}{\zeta}\sqrt{(\zeta-a)(\zeta-b)} \end{eqnarray*} となり $\zeta=0$ は分岐点ではなく極となる。このことから、無限遠点は $w=\sqrt{(z-a)(z-b)}$ の分岐点でないことがわかる（無限遠点が分岐点でない例）。

　以上より、切断としては $z=a$ と $z=b$ を結ぶ曲線を考えればよい。$z=a$ と $z=b$ の結び方は任意であるので、図8に示すような様々な曲線が考えられるが、計算に都合のいいものを選べばよい。

図8 $w=\sqrt{(z-a)(z-b)}$ の切断（赤実線）の例

　図8 (iii),(iv) は無限遠点を介して $z=a$ と $z=b$ が結ばれている切断の例である。通常は $w=\sqrt{(z-a)(z-b)}$ の切断として図8 (i), (iii) が用いられる [2]。

　図8 (i) の切断に対するリーマン面は、2 枚の $z$ 平面 $S_{1},\,S_{2}$ 上に $z=a,\,z=b$ を結ぶ線に沿って切断を作り、切断に沿って $S_{1}$ の切り口の下端と $S_{2}$ の切り口の上端をつなげ、$S_{2}$ の下端と $S_{1}$ の上端とをつないだものとして得られる（図9 (i)）。同様に、図8 (iii) の切断に対するリーマン面は、2 枚の $z$ 平面 $S_{1},\,S_{2}$ 上に $z=a,\,z=\infty$ を結ぶ線 $z=b,\,z=\infty$ とに沿って切断を作り、切断に沿って $S_{1}$ の切り口の下端と $S_{2}$ の切り口の上端をつなげ、$S_{2}$ の下端と $S_{1}$ の上端とをつないだものとして得られる（図9 (ii)）。

図9 $w=\sqrt{(z-a)(z-b)}$ に対するリーマン面

　もう1つの例として、ベッセル関数の積分表示を考える際に必要となる関数 \begin{equation} w=(z^{2}-1)^{1/4}=(z-1)^{1/4}(z+1)^{1/4}\label{eq:5} \end{equation} について考える。 \begin{eqnarray*} z-1 & = & \alpha e^{i(\theta+2n\pi)}\\ z+1 & = & \beta e^{i(\varphi+2m\pi)} \end{eqnarray*} とおけば \begin{eqnarray*} w & = & (\alpha\beta)^{1/4}e^{i(\theta+\varphi+2\pi(n+m))/4}\\ & = & (\alpha\beta)^{1/4}e^{i\pi(n+m)/2}e^{i(\theta+\varphi)/4} \end{eqnarray*} であるので、$n+m=4k\;(k\in\mathbb{Z})$ のとき $w$ は元の値に戻る。$z=1$ の周りに 4 周 $(n=4,\ m=0)$ または $z=-1$ の周りに 4 周 $(n=0,\ m=4)$ すれば元に戻るので、$z=\pm1$ は 3 位の分岐点である。加えて、$z=1/\zeta$ とおくと \[ w=\left(\dfrac{1}{\zeta^{2}}-1\right)^{1/4}=\zeta^{-1/2}(1-\zeta^{2})^{1/4} \] となり、$\zeta=0$ すなわち $z=\infty$（無限遠点）は 1 位の分岐点となっている。よって、式(\ref{eq:5})の $w$ は、$z=\pm1$ および $z=\infty$ に 1 位の分岐点をもつ関数であることがわかる。そのため切断としては、$z=1$ と $z=\infty$ を結ぶ曲線と $z=-1$ と $z=\infty$ を結ぶ曲線の 2 つを選ぶことになる。ベッセル関数の積分表示を考える際には図10のような切断が使用される [1]。

図10 $w=(z^{2}-1)^{1/4}$ の切断の例

　分岐点がある複素関数を積分する場合の注意点について例を用いて説明する。分枝を考慮して、次の積分を求めることを考える。 \[ I=\int_{0}^{\infty}\dfrac{\sqrt{x}}{1+x^{2}}dx \] 分岐がある複素関数を積分する場合、分岐点からの切断を定め、その両側での複素数 $z$ の位相を厳密に指定する必要がある。ここでは、まず実軸上の $0\rightarrow\infty$ を含むある積分路 $C$ についての周積分 \[ \oint_{C}\dfrac{\sqrt{z}}{1+z^{2}}dz \] を考え、その積分路 $C$ を適当に選ぶ。この被積分関数の特異点は、以下の4つである：(a) $z=i$ に 1 位の極、(b) $z=-i$ の 1 位の極、(c) $z=0$ の 1 位の分岐点、(d) $z=\infty$ の 1 位の分岐点である。被積分関数において $z=1/\zeta$ とおくと \[ \dfrac{\sqrt{z}}{1+z^{2}}=\dfrac{\zeta^{3/2}}{\zeta^{2}+1} \] となることから、$\zeta=0\,(z=\infty)$が1位の分岐点であることがわかる。

　2 つの極については留数定理で扱えるが、分岐点 $z=0$ と $z=\infty$ を結ぶ切断をどのように定めるかが問題となる。切断の定め方は任意であるが、積分路 $C$ は $0\rightarrow+\infty $を含む必要があるので、計算に都合のよいように $z=0$ から正の実軸上に切断を伸ばすことにする（図11）。

図11 積分路 $C$

　次に、$+\infty$ につながる無限遠方の円周部分（ $C'$ とする）をどのようにとるかを考える。位相 $\theta_{1}\rightarrow\theta_{2}$ の円弧とし、$z=Re^{i\theta}$ とおくと、$dz=iRe^{i\theta}d\theta$ より、$R\rightarrow\infty$ で \begin{eqnarray*} \oint_{C'}\dfrac{\sqrt{z}}{1+z^{2}}dz & = & \int_{\theta_{1}}^{\theta_{2}}\dfrac{\sqrt{R}e^{i\theta/2}}{1+R^{2}e^{2i\theta}}iRe^{i\theta}d\theta\\ & \rightarrow & \int_{\theta_{1}}^{\theta_{2}}\dfrac{iR\sqrt{R}e^{i3\theta/2}}{R^{2}e^{2i\theta}}d\theta=\dfrac{1}{\sqrt{R}}\int_{\theta_{1}}^{\theta_{2}}e^{-i\theta/2}d\theta\rightarrow0\quad(R\rightarrow\infty) \end{eqnarray*} となる。$\theta_{1}$ や $\theta_{2}$ にかかわらずどの範囲でも 0 になるので、実軸上の切断の位置から、$\theta=0\rightarrow2\pi$ の 1 周とする。よって積分路 $C$ は図10のようにする。 \[ \oint_{C}\dfrac{\sqrt{z}}{1+z^{2}}dz=\left(\int_{C_{1}}+\int_{C_{2}}+\int_{C_{3}}+\int_{C_{4}}\right)\dfrac{\sqrt{z}}{1+z^{2}}dz \] となり、すでに $\int_{C_{2}}\rightarrow0\;(R\rightarrow\infty)$ は示した。また半円 $C_{4}$ については $z=\epsilon e^{i\theta}$ で $\epsilon\rightarrow0$ とすると \begin{eqnarray*} \oint_{C_{4}}\dfrac{\sqrt{z}}{1+z^{2}}dz & = & \int_{2\pi}^{0}\dfrac{\sqrt{\epsilon}e^{i\theta/2}}{1+\epsilon^{2}e^{2i\theta}}i\epsilon e^{i\theta}d\theta\\ & \rightarrow & i\epsilon^{3/2}\int_{2\pi}^{0}e^{3i\theta/2}d\theta\rightarrow0\quad(\epsilon\rightarrow0) \end{eqnarray*} と 0 になる。よって、$C_{1}$ と $C_{3}$ 上の積分だけが残る。これらの積分は切断の上と下の積分なので、$z=xe^{i\theta}$ の位相 $\theta$ を厳密に定義する必要がある。今、$x=0\rightarrow\infty$ の積分を求めたいので、$C_{1}$ をこれに対応させ、$C_{1}$ で $\theta=0$ とする。 \[ \int_{C_{1}}\dfrac{\sqrt{z}}{1+z^{2}}dz=\int_{0}^{\infty}\dfrac{\sqrt{x}e^{i\theta/2}}{1+x^{2}e^{2i\theta}}e^{i\theta}dx\Bigg|_{\theta=0}=\int_{0}^{\infty}\dfrac{\sqrt{x}}{1+x^{2}}dx \] $C_{1}$ 上で $\theta=0$ ならば、$C_{3}$ は切断を横切らない経路 $C$ の一部なので、$C_{3}$ 上では $\theta=2\pi$ としなければならないので \[ \int_{C_{3}}\dfrac{\sqrt{z}}{1+z^{2}}dz=\int_{\infty}^{0}\dfrac{\sqrt{x}e^{i\theta/2}}{1+x^{2}e^{2i\theta}}e^{i\theta}dx\Bigg|_{\theta=2\pi}=\int_{\infty}^{0}\dfrac{\sqrt{x}e^{3\pi i}}{1+x^{2}}dx=\int_{0}^{\infty}\dfrac{\sqrt{x}}{1+x^{2}}dx \] よって、$C$ についての周積分は、以下のようになることが示された： \[ \oint_{C}\dfrac{\sqrt{z}}{1+z^{2}}dz=\left(\int_{C_{1}}+\int_{C_{3}}\right)\dfrac{\sqrt{z}}{1+z^{2}}dz=2\int_{0}^{\infty}\dfrac{\sqrt{x}}{1+x^{2}}dx=2I \]

　一方、$C$ の内部には $z=\pm i$（ただし、上の位相の定義より $i=e^{i\pi/2},\,-i=e^{3i\pi/2}$ と定める必要がある）の極があるので、この積分は留数定理より \begin{eqnarray*} \oint_{C}\dfrac{\sqrt{z}}{1+z^{2}}dz & = & 2\pi i\left[\mathrm{Res}(z=i)+\mathrm{Res}(z=-i)\right]\\ & = & 2\pi i\left[\left((z-i)\dfrac{\sqrt{z}}{1+z^{2}}\right)\Bigg|_{z=e^{i\pi/2}}+\left((z+i)\dfrac{\sqrt{z}}{1+z^{2}}\right)\Bigg|_{z=e^{i3\pi/2}}\right]\\ & = & 2\pi i\left[\dfrac{e^{i\pi/4}}{i+e^{i\pi/2}}+\dfrac{e^{i3\pi/4}}{-i+e^{i3\pi/2}}\right]\\ & = & 2\pi i\left[\dfrac{e^{i\pi/4}}{2i}+\dfrac{e^{i3\pi/4}}{-2i}\right]\\ & = & \pi\left[e^{i\pi/4}-e^{i3\pi/4}\right]\\ & = & \pi\left[\dfrac{1+i}{\sqrt{2}}-\dfrac{-1+i}{\sqrt{2}}\right]=\pi\sqrt{2} \end{eqnarray*} となる。よって \[ I=\dfrac{\pi}{\sqrt{2}} \] となる。

　最後に、関数の特異点と分岐点の関係について述べる。特異点は大別すると、分岐を伴う特異点 (分岐点) と、分岐を伴わない特異点とに分けられる。複素平面上の関数が孤立した点 $s$ に特異点を持つとき、その関数は特異点 $s$ を中心に級数展開すると、大抵次のような関数項が現れ、分岐点と以下のように関係している。

1) 寺沢寛一　『自然科学者のための数学概論　増訂版』 p.180 岩波書店 (1983/05/18)

2) 蓬田 清　『演習形式で学ぶ特殊関数・積分変換入門』 p.18 共立出版 (2007/09/25)

3) 洲之内 治男、猪股 清二『関数論 (サイエンスライブラリ理工系の数学 3) 』 p.116 サイエンス社 (1978/05/20)