光の角運動量と運動量
『平面波の場のなかの電荷の運動』[1] では、円偏光した平面電磁波による自由電荷の運動を考えることにより電磁波の角運動量について考察した。ここでは、『ファインマン物理学 II 光、熱、波動』[2] にしたがって光(電磁波)の角運動量、運動量についてもう一度考察する。
1. 光の角運動量
円偏光した光(平面電磁波)が原子中の減衰をともなって単振動すると考えられる電荷にあたる場合を考える(注1)。電磁場中での電荷の運動方程式は、ガウス単位系では
\begin{equation}
\begin{aligned}\dfrac{d\boldsymbol{p}}{dt} & =-m\omega_{0}^{2}\boldsymbol{r}-m\gamma\boldsymbol{v}+e\boldsymbol{E}+\dfrac{e}{c}\boldsymbol{v}\times\boldsymbol{H}\\
\boldsymbol{p} & =\dfrac{m\boldsymbol{v}}{\sqrt{1-\left(\dfrac{v}{c}\right)^{2}}}
\end{aligned}
\label{eq:1}
\end{equation}
と与えられる。ここで、$\boldsymbol{r},\,\boldsymbol{v},\,\boldsymbol{p}$ はそれぞれ電荷の位置、速度、運動量ベクトルであり、$\omega_{0},\,\gamma$ はそれぞれ単振動の角振動数、減衰(抵抗)の大きさを表す減衰係数である。
また、左回りの円偏光した角振動数 $\omega$、波数 $k$ で $z$ 軸方向に伝播する平面電磁波の電場 $\boldsymbol{E}$ と磁場 $\boldsymbol{H}$ は
\begin{equation}
\begin{aligned}\boldsymbol{E}(z,\,t) & =\begin{pmatrix}E_{x}(z,\,t)\\
E_{y}(z,\,t)\\
E_{z}(z,\,t)
\end{pmatrix}=\begin{pmatrix}E_{0}\cos\left(\omega t-kz\right)\\
E_{0}\sin\left(\omega t-kz\right)\\
0
\end{pmatrix}\\
\boldsymbol{H}(z,\,t) & =\begin{pmatrix}B_{x}(z,\,t)\\
B_{y}(z,\,t)\\
B_{z}(z,\,t)
\end{pmatrix}=\begin{pmatrix}-E_{0}\sin\left(\omega t-kz\right)\\
E_{0}\cos\left(\omega t-kz\right)\\
0
\end{pmatrix}
\end{aligned}
\label{eq:2}
\end{equation}
と表される [1,3,4]。
以下では、電荷の速度が光速に比べて十分に小さく、$v/c\ll1$ とみなせる非相対論的な場合について考える。この近似では式(\ref{eq:1})の運動量は
\[
\boldsymbol{p}\doteqdot m\boldsymbol{v}
\]
となる。また、磁場 $\boldsymbol{H}$ によるローレンツ力の寄与は電場 $\boldsymbol{E}$ からの寄与に比べて無視することがでる。したがって、第 0 近似では式(\ref{eq:1})の $x,\,y$成分 は
\begin{eqnarray}
m\dfrac{d^{2}x}{dt^{2}} & = & -m\omega_{0}^{2}x-m\gamma\dfrac{dx}{dt}+eE_{0}\cos\left(\omega t-kz\right)\label{eq:3}\\
m\dfrac{d^{2}y}{dt^{2}} & = & -m\omega_{0}^{2}y-m\gamma\dfrac{dy}{dt}+eE_{0}\sin\left(\omega t-kz\right)\label{eq:4}
\end{eqnarray}
となる。$z$ 方向については、電場による力が働かないため単振動はせず
\begin{eqnarray}
m\dfrac{d^{2}z}{dt^{2}} & = & \dfrac{e}{c}\left(v_{x}H_{y}-v_{y}H_{x}\right)\nonumber \\
& = & eE_{0}\left(\dfrac{v_{x}}{c}\cos\left(\omega t-kz\right)+\dfrac{v_{y}}{c}\sin\left(\omega t-kz\right)\right)\label{eq:5}
\end{eqnarray}
と表されるものとする。第 0 近似としては式(\ref{eq:5})は
\begin{equation}
m\dfrac{d^{2}z}{dt^{2}}=0\label{eq:6}
\end{equation}
と近似できる(光の運動量を考える際には式(\ref{eq:5})の右辺の影響を考慮することになる)。
初期条件として、電荷は時刻$t=0$で原点に静止していたとする。すなわち
\begin{equation}
t=0\;:\;\boldsymbol{r}=\dfrac{d\boldsymbol{r}}{dt}=0\label{eq:7}
\end{equation}
この場合、式(\ref{eq:6})より
\[
z(t)=0
\]
と定まるので、式(\ref{eq:3})、(\ref{eq:4})は
\begin{eqnarray}
m\dfrac{d^{2}x}{dt^{2}} & = & -m\omega_{0}^{2}x-m\gamma\dfrac{dx}{dt}+eE_{0}\cos\omega t\label{eq:8}\\
m\dfrac{d^{2}y}{dt^{2}} & = & -m\omega_{0}^{2}y-m\gamma\dfrac{dy}{dt}+eE_{0}\sin\omega t\label{eq:9}
\end{eqnarray}
となる。式(\ref{eq:8})、(\ref{eq:9})は減衰をともなった単振動に対する強制振動の運動方程式となっている。式(\ref{eq:8})、(\ref{eq:9})を
\begin{eqnarray}
\dfrac{d^{2}x}{dt^{2}}+\gamma\dfrac{dx}{dt}+\omega_{0}^{2}x & = & \dfrac{eE_{0}}{m}\cos\omega t\label{eq:10}\\
\dfrac{d^{2}y}{dt^{2}}+\gamma\dfrac{dy}{dt}+\omega_{0}^{2}y & = & \dfrac{eE_{0}}{m}\sin\omega t\label{eq:11}
\end{eqnarray}
と書けば、非同次定数係数 2 階微分方程式に相当するので、初期条件(\ref{eq:7})に対する解は
\begin{eqnarray}
x(t) & = & \dfrac{1}{\lambda_{1}-\lambda_{2}}\left(\left(F_{2}-\lambda_{2}F_{1}\right)e^{\lambda_{1}t}-\left(F_{2}-\lambda_{1}F_{1}\right)e^{\lambda_{2}t}\right)\nonumber \\
& & +\dfrac{eE_{0}}{m}\dfrac{1}{\sqrt{\gamma^{2}\omega^{2}+\left(\omega^{2}-\omega_{0}^{2}\right)^{2}}}\begin{cases}
\cos\left(\omega t+\delta+\pi\right) & \omega^{2}-\omega_{0}^{2}>0\\
\cos\left(\omega t+\delta\right) & \omega^{2}-\omega_{0}^{2}< 0
\end{cases}\label{eq:12}\\
y(t) & = & \dfrac{1}{\lambda_{1}-\lambda_{2}}\left(\left(F_{4}-\lambda_{2}F_{3}\right)e^{\lambda_{1}t}-\left(F_{4}-\lambda_{1}F_{3}\right)e^{\lambda_{2}t}\right)\nonumber \\
& & +\dfrac{eE_{0}}{m}\dfrac{1}{\sqrt{\gamma^{2}\omega^{2}+\left(\omega^{2}-\omega_{0}^{2}\right)^{2}}}\begin{cases}
\sin\left(\omega t+\delta+\pi\right) & \omega^{2}-\omega_{0}^{2}>0\\
\sin\left(\omega t+\delta\right) & \omega^{2}-\omega_{0}^{2}< 0
\end{cases}\label{eq:13}\\
\delta & = & \tan^{-1}\left(\dfrac{\gamma\omega}{\omega^{2}-\omega_{0}^{2}}\right)
\end{eqnarray}
となる [5]。ここで
\begin{eqnarray}
\lambda_{1} & = & \dfrac{1}{2}\left(-\gamma+\sqrt{\gamma^{2}-4\omega_{0}^{2}}\right)\label{eq:15}\\
\lambda_{2} & = & \dfrac{1}{2}\left(-\gamma-\sqrt{\gamma^{2}-4\omega_{0}^{2}}\right)\label{eq:16}\\
F_{1} & = & \dfrac{\omega^{2}-\omega_{0}^{2}}{\gamma^{2}\omega^{2}+\left(\omega^{2}-\omega_{0}^{2}\right)^{2}}\dfrac{eE_{0}}{m}\nonumber \\
F_{2} & = & \dfrac{-\gamma\omega^{2}}{\gamma^{2}\omega^{2}+\left(\omega^{2}-\omega_{0}^{2}\right)^{2}}\dfrac{eE_{0}}{m}\nonumber \\
F_{3} & = & -\dfrac{F_{2}}{\omega}\nonumber \\
F_{4} & = & \omega F_{1}\nonumber
\end{eqnarray}
である。
減衰係数 $\gamma$ が正( $\gamma>0$ )であれば、式(\ref{eq:15})、(\ref{eq:16})の $\lambda_{1},\,\lambda_{2}$ は負となり( $\lambda_{1}< 0,\,\lambda_{2}< 0$ )、十分に時間が経過すれば式(\ref{eq:12})、(\ref{eq:13})における指数関数部分は0となり、$x(t),\,y(t)$ は
\begin{eqnarray}
x(t) & \doteqdot & \begin{cases}
R_{0}\cos\left(\omega t+\delta+\pi\right) & \omega^{2}-\omega_{0}^{2}>0\\
R_{0}\cos\left(\omega t+\delta\right) & \omega^{2}-\omega_{0}^{2}< 0
\end{cases}\label{eq:17}\\
y(t) & \doteqdot & \begin{cases}
R_{0}\sin\left(\omega t+\delta+\pi\right) & \omega^{2}-\omega_{0}^{2}>0\\
R_{0}\sin\left(\omega t+\delta\right) & \omega^{2}-\omega_{0}^{2}< 0
\end{cases}\label{eq:18}\\
R_{0} & = & \dfrac{eE_{0}}{m}\dfrac{1}{\sqrt{\gamma^{2}\omega^{2}+\left(\omega^{2}-\omega_{0}^{2}\right)^{2}}}\\
\delta & = & \tan^{-1}\left(\dfrac{\gamma\omega}{\omega^{2}-\omega_{0}^{2}}\right)\label{eq:20}
\end{eqnarray}
と近似できる。式(\ref{eq:17})、(\ref{eq:18})より、電荷は $xy$ 平面内で光の角振動数 $\omega$ に対応した角振動数 $\omega$、半径 $R_{0}$ の等速円運動を行うことがわかる。左回りの円偏光に対応して、電荷も左回り(反時計回り)に回転する。ただし、減衰(抵抗)の影響を考えているので、その位相は光の位相から $\delta$ または $\delta+\pi$ だけずれている。式(\ref{eq:12})、(\ref{eq:13})から求めた左回りの円偏光による電荷の運動の様子を図1に示す。原点に静止していた電荷が左回りの円偏光した電場によって、左回りに回転し、十分時間が経過すると円軌道を運動する様子がわかる。

図1 左回りの円偏光による電荷の運動の様子 $(\mathrm{a})\,\omega^{2}-\omega_{0}^{2}>0,\,(\mathrm{b})\,\omega^{2}-\omega_{0}^{2}< 0$
電荷の位置ベクトル $\boldsymbol{r}$ と電場ベクトル $\boldsymbol{E}$ の関係を図2に示す。減衰による位相のずれにより、電荷の位置ベクトル $\boldsymbol{r}$ と電場ベクトル $\boldsymbol{E}$ は平行ではなく、位置ベクトル $\boldsymbol{r}$ に垂直な電場ベクトル $\boldsymbol{E}$ の成分が存在する。この成分が電荷に仕事をし、電荷にトルク $\boldsymbol{\tau}$ すなわち角運動量を与えることになる。

図2 電荷の位置ベクトル $\boldsymbol{r}$ と電場ベクトル $\boldsymbol{E}$ の関係
1.1 電磁波が電荷に与える単位時間当たりのエネルギー
式(\ref{eq:17})、(\ref{eq:18})より、電荷の速度の $x,\,y$ 成分は
\begin{eqnarray}
v_{x}(t) & \doteqdot & \begin{cases}
-\omega R_{0}\sin\left(\omega t+\delta+\pi\right) & \omega^{2}-\omega_{0}^{2}>0\\
-\omega R_{0}\sin\left(\omega t+\delta\right) & \omega^{2}-\omega_{0}^{2}< 0
\end{cases}\label{eq:21}\\
v_{y}(t) & \doteqdot & \begin{cases}
\omega R_{0}\cos\left(\omega t+\delta+\pi\right) & \omega^{2}-\omega_{0}^{2}>0\\
\omega R_{0}\cos\left(\omega t+\delta\right) & \omega^{2}-\omega_{0}^{2}< 0
\end{cases}\label{eq:22}
\end{eqnarray}
となる。電磁波が電荷にする単位時間当たりの仕事(仕事率)$W$ は
\[
W=e\boldsymbol{E}\cdot\boldsymbol{v}
\]
と表される。したがって、$\omega^{2}-\omega_{0}^{2}>0$ に対しては(式(\ref{eq:20})より $\delta>0$ )
\begin{eqnarray}
W & = & e\omega E_{0}R_{0}\left(-\cos\omega t\,\sin\left(\omega t+\delta+\pi\right)+\sin\omega t\,\cos\left(\omega t+\delta+\pi\right)\right)\nonumber \\
& = & e\omega E_{0}R_{0}\bigg(-\cos\omega t\,\left(\sin\omega t\,\cos\left(\delta+\pi\right)+\cos\omega t\,\sin\left(\delta+\pi\right)\right)\nonumber \\
& & \qquad\qquad+\sin\omega t\,\left(\cos\omega t\,\cos\left(\delta+\pi\right)-\sin\omega t\,\sin\left(\delta+\pi\right)\right)\bigg)\nonumber \\
& = & -e\omega E_{0}R_{0}\sin\left(\delta+\pi\right)\nonumber \\
& = & e\omega E_{0}R_{0}\sin\delta>0\label{eq:23}
\end{eqnarray}
同様に、$\omega^{2}-\omega_{0}^{2}< 0$ に対しては(式(\ref{eq:20})より $\delta< 0$ )
\begin{eqnarray}
W & = & e\omega E_{0}R_{0}\left(-\cos\omega t\,\sin\left(\omega t+\delta\right)+\sin\omega t\,\cos\left(\omega t+\delta\right)\right)\nonumber \\
& = & e\omega E_{0}R_{0}\bigg(-\cos\omega t\,\left(\sin\omega t\,\cos\delta+\cos\omega t\,\sin\delta\right)\nonumber \\
& & \qquad\qquad+\sin\omega t\,\left(\cos\omega t\,\cos\delta-\sin\omega t\,\sin\delta\right)\bigg)\nonumber \\
& = & -e\omega E_{0}R_{0}\sin\delta\nonumber \\
& = & e\omega E_{0}R_{0}\sin(-\delta)>0\label{eq:24}
\end{eqnarray}
となる。
式(\ref{eq:23})、(\ref{eq:24})より、電荷は単位時間当たり$W$の仕事を受け取ったことになり、電荷のエネルギーを $\mathcal{E}$ とすれば、単位時間当たりのエネルギーの増加は
\begin{equation}
\dfrac{d\mathcal{E}}{dt}=W=\begin{cases}
\omega eE_{0}R_{0}\sin\delta & \omega^{2}-\omega_{0}^{2}>0\\
\omega eE_{0}R_{0}\sin(-\delta) & \omega^{2}-\omega_{0}^{2}< 0
\end{cases}\label{eq:25}
\end{equation}
と表される。このことは電荷に吸収された光(電磁波)は、同じエネルギー $\mathcal{E}$ をもっていたことを示している。
1.2 電磁波が電荷に与えるトルク
電磁波が電荷に与えるトルクは
\begin{equation}
\boldsymbol{\tau}=\boldsymbol{r}\times\left(e\boldsymbol{E}\right)=\begin{pmatrix}x\\
y\\
0
\end{pmatrix}\times\begin{pmatrix}eE_{x}\\
eE_{y}\\
0
\end{pmatrix}=\begin{pmatrix}0\\
0\\
e\left(xE_{y}-yE_{x}\right)
\end{pmatrix}\label{eq:26}
\end{equation}
と表される。ここで、$\omega^{2}-\omega_{0}^{2}>0$ に対しては(式(\ref{eq:20})より $\delta>0 $)
\begin{eqnarray}
xE_{y}-yE_{x} & = & E_{0}R_{0}\left(\cos\left(\omega t+\delta+\pi\right)\sin\omega t-\sin\left(\omega t+\delta+\pi\right)\cos\omega t\right)\nonumber \\
& = & E_{0}R_{0}\bigg(\left(\cos\omega t\,\cos\left(\delta+\pi\right)-\sin\omega t\,\sin\left(\delta+\pi\right)\right)\sin\omega t\nonumber \\
& & \qquad\qquad-\left(\sin\omega t\,\cos\left(\delta+\pi\right)+\cos\omega t\,\sin\left(\delta+\pi\right)\right)\cos\omega t\bigg)\nonumber \\
& = & -E_{0}R_{0}\sin\left(\delta+\pi\right)\nonumber \\
& = & E_{0}R_{0}\sin\delta>0
\end{eqnarray}
同様に、$\omega^{2}-\omega_{0}^{2}< 0$ に対しては(式(\ref{eq:20})より $\delta< 0$ )
\begin{eqnarray}
xE_{y}-yE_{x} & = & E_{0}R_{0}\left(\cos\left(\omega t+\delta\right)\sin\omega t-\sin\left(\omega t+\delta\right)\cos\omega t\right)\nonumber \\
& = & E_{0}R_{0}\bigg(\left(\cos\omega t\,\cos\delta-\sin\omega t\,\sin\delta\right)\sin\omega t\nonumber \\
& & \qquad\qquad-\left(\sin\omega t\,\cos\delta+\cos\omega t\,\sin\delta\right)\cos\omega t\bigg)\nonumber \\
& = & -E_{0}R_{0}\sin\delta\nonumber \\
& = & E_{0}R_{0}\sin(-\delta)>0
\end{eqnarray}
となることから、式(\ref{eq:26})のトルクの $z$ 成分は
\begin{equation}
\tau_{z}=eE_{0}R_{0}\begin{cases}
\sin\delta & \omega^{2}-\omega_{0}^{2}>0\\
\sin(-\delta) & \omega^{2}-\omega_{0}^{2}< 0
\end{cases}\label{eq:29}
\end{equation}
となる。式(\ref{eq:29})より $\tau_{z}>0$ であることから、$z$ 方向に伝播する左回りに偏光した電磁波からは伝播方向のトルクを受けることになる。この電磁波からのトルクによって、電荷は減衰(抵抗)の影響を受けているにもかかわらず、等速円運動を続けることができている。
このことは、電磁波が単位時間当たり $\tau_{z}$ の角運動量を電荷に与えていることになる。すなわち、電磁波は
\begin{equation}
\dfrac{dL_{z}}{dt}=\tau_{z}\label{eq:30}
\end{equation}
に対応する角運動量 $L_{z}$ を電荷に与えた(円偏光した電磁波は角運動量をもつ)ことを意味する。
1.3 電磁波のエネルギーと角運動量の関係
式(\ref{eq:25})と式(\ref{eq:30})の比をとると、式(\ref{eq:29})より
\[
\dfrac{\dfrac{d\mathcal{E}}{dt}}{\dfrac{dL_{z}}{dt}}=\dfrac{W}{\tau_{z}}=\omega
\]
となる。これより
\[
\mathcal{E}=\omega L_{z}
\]
すなわち
\begin{equation}
L_{z}=\dfrac{\mathcal{E}}{\omega}\label{eq:31}
\end{equation}
の関係を得る。かくして、全エネルギー $\mathcal{E}$ を含む $z$ 方向に伝播する左回りの円偏光の電磁波は角運動量
\[
L_{z}=\dfrac{\mathcal{E}}{\omega}
\]
をもっていることがわかる(角運動量の方向は電磁波の伝播方向に向かっている)。この電磁波が電荷に吸収されると、この角運動量は電荷に移る。なお、右回りの円偏光は反対の符号の
\begin{equation}
L_{z}=-\dfrac{\mathcal{E}}{\omega}\label{eq:32}
\end{equation}
の角運動量をもつ [2,6](注2)。
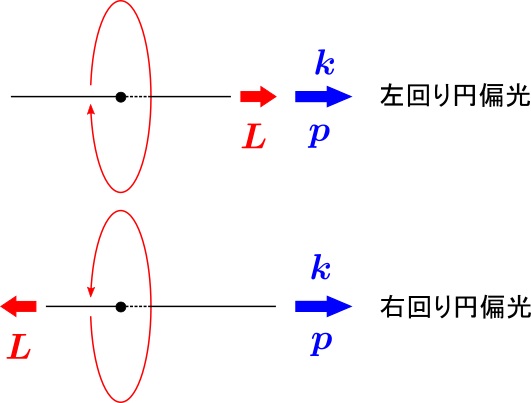
図3 円偏光した電磁波の角運動量 $\boldsymbol{L}$ と運動量 $\boldsymbol{p}$
2. 光の運動量
これまで光(電磁波)に付随する磁場の効果については、全然触れなかった。通常、光(電磁波)における磁場の効果はきわめて小さいが、磁場による重要な現象が 1 つ存在する。電磁波の電場により電荷の速度が生じると、磁場は電荷に力を及ぼすことになる(磁場は電荷が動いているときにだけ力を及ぼす)。その力の向きは、$z=0$ において
\[
\boldsymbol{v}(t)=\begin{pmatrix}v_{x}(t)\\
v_{y}(t)\\
0
\end{pmatrix}
\]
となる第 0 近似においては、式(\ref{eq:5})に示すように
\[
\boldsymbol{F}=\dfrac{e}{c}\boldsymbol{v}\times\boldsymbol{H}=\dfrac{e}{c}\begin{pmatrix}v_{x}(t)\\
v_{y}(t)\\
0
\end{pmatrix}\times\begin{pmatrix}-E_{0}\sin\omega t\\
E_{0}\cos\omega t\\
0
\end{pmatrix}=\dfrac{eE_{0}}{c}\begin{pmatrix}0\\
0\\
v_{x}(t)\cos\omega t+v_{y}(t)\sin\omega t
\end{pmatrix}
\]
より、光(電磁波)の進行方向となる。すなわち、電荷が光に照らされ、それによって振動しているとき、電荷には光(電磁波)の伝播方向におしやる力が働くことになる。これが輻射圧とか光の圧力と呼ばれるものである。この場合の輻射圧の大きさは
\begin{eqnarray*}
|\boldsymbol{F}|=F_{z} & = & \dfrac{eE_{0}}{c}\left(v_{x}(t)\cos\omega t+v_{y}(t)\sin\omega t\right)
\end{eqnarray*}
となる。ここで、式(\ref{eq:21})、(\ref{eq:22})を代入すれば、$\omega^{2}-\omega_{0}^{2}>0$ に対しては(式(\ref{eq:20})より $\delta>0$ )
\begin{eqnarray}
F_{z} & = & -\dfrac{\omega eE_{0}R_{0}}{c}\left(\sin\left(\omega t+\delta+\pi\right)\cos\omega t-\cos\left(\omega t+\delta+\pi\right)\sin\omega t\right)\nonumber \\
& = & -\dfrac{\omega eE_{0}R_{0}}{c}\bigg(\left(\sin\omega t\cos\left(\delta+\pi\right)+\cos\omega t\sin\left(\delta+\pi\right)\right)\cos\omega t\nonumber \\
& & \qquad-\left(\cos\omega t\cos\left(\delta+\pi\right)-\sin\omega t\sin\left(\delta+\pi\right)\right)\sin\omega t\nonumber \\
& = & -\dfrac{\omega eE_{0}R_{0}}{c}\sin\left(\delta+\pi\right)\nonumber \\
& = & \dfrac{\omega eE_{0}R_{0}}{c}\sin\delta>0
\end{eqnarray}
$\omega^{2}-\omega_{0}^{2}< 0$ に対しては(式(\ref{eq:20})より $\delta< 0$ )
\begin{eqnarray}
F_{z} & = & -\dfrac{\omega eE_{0}R_{0}}{c}\left(\sin\left(\omega t+\delta\right)\cos\omega t-\cos\left(\omega t+\delta\right)\sin\omega t\right)\nonumber \\
& = & -\dfrac{\omega eE_{0}R_{0}}{c}\bigg(\left(\sin\omega t\cos\delta+\cos\omega t\sin\delta\right)\cos\omega t\nonumber \\
& & \qquad-\left(\cos\omega t\cos\delta-\sin\omega t\sin\delta\right)\sin\omega t\nonumber \\
& = & -\dfrac{\omega eE_{0}R_{0}}{c}\sin\delta\nonumber \\
& = & \dfrac{\omega eE_{0}R_{0}}{c}\sin(-\delta)>0
\end{eqnarray}
となる。したがって、単位時間当たりの $z$ 方向の運動量の変化量は
\begin{equation}
\dfrac{dp_{z}}{dt}=F_{z}=\begin{cases}
\dfrac{\omega eE_{0}R_{0}}{c}\sin\delta & \omega^{2}-\omega_{0}^{2}>0\\
\dfrac{\omega eE_{0}R_{0}}{c}\sin(-\delta) & \omega^{2}-\omega_{0}^{2}< 0
\end{cases}
\end{equation}
となる。ここで、式(\ref{eq:25})との比を考えれば
\[
\dfrac{\dfrac{d\mathcal{E}}{dt}}{\dfrac{dp_{z}}{dt}}=\dfrac{W}{F_{z}}=c
\]
すなわち
\begin{equation}
p_{z}=\dfrac{\mathcal{E}}{c}\label{eq:36}
\end{equation}
となる。電荷は光(電磁波)から $\dfrac{\mathcal{E}}{c}$ の大きさの運動量を与えられることになる。言い換えれば、光(電磁波)は伝播方向に $\dfrac{\mathcal{E}}{c}$ の大きさの運動量をもつことになる。
3. 量子論との関係
ここまでの古典電磁気学の範囲内での結果をまとめると、$z$ 方向に伝播する角振動数 $\omega$ の円偏光した光(電磁波)は、$z$ 方向の角運動量 $L_{z}$ と運動量 $p_{z}$ をもち、その大きさは光のエネルギーを $\mathcal{E}$ とすれば
\begin{equation}
\begin{cases}
L_{z}=\dfrac{\mathcal{E}}{\omega} & \text{:左回りの円偏光}\\
L_{z}=-\dfrac{\mathcal{E}}{\omega} & \text{:右回りの円偏光}\\
p_{z}=\dfrac{\mathcal{E}}{c}
\end{cases}
\end{equation}
となる。これが光の古典論の立場で言える限界である。量子論では、角振動数 $\omega$ の単色の電磁波は、エネルギー $E=\hbar\omega$ の光子の集まりであると考えられている。ここで、$h$ をプランク定数として、$\hbar=h/2\pi$ である。以下では、量子論的観点から考察する [2,7,8]。
まず、電荷が吸収する光子の数を考える。光子 1 個当たりのエネルギーは $\hbar\omega$ であるから、電荷が吸収する光子の数$N$は光(電磁波)が電荷に与えたエネルギー $\mathcal{E}$ を $\hbar\omega$ で割ることで
\begin{equation}
N=\dfrac{\mathcal{E}}{\hbar\omega}
\end{equation}
として求められる。これより左回りに円偏光した $z$ 方向に伝播する光(電磁波)のエネルギーは
\begin{equation}
\mathcal{E}=N\hbar\omega
\end{equation}
と表すこともできる。したがって、式(\ref{eq:31})より、光(電磁波)の角運動量は
\[
L_{z}=\dfrac{\mathcal{E}}{\omega}=N\hbar
\]
となる。よって、光子 1 個あたりの角運動量を $S_{z}$ とすれば
\[
S_{z}=\dfrac{L_{z}}{N}=\hbar
\]
となる。すなわち、左回りに円偏光した光(電磁波)を形成する光子1個あたりの角運動量は $\hbar$ となる。一方、式(\ref{eq:32})より、右回りに円偏光した光(電磁波)を形成する光子 1 個あたりの角運動量は $-\hbar$ となる。
\begin{equation}
S_{z}=\begin{cases}
\hbar & \text{左回りに円偏光}\\
-\hbar & \text{右回りに円偏光}
\end{cases}\label{eq:40}
\end{equation}
同様に、式(\ref{eq:36})より、光(電磁波)の運動量は
\[
p_{z}=\dfrac{\mathcal{E}}{c}=\dfrac{N\hbar\omega}{c}
\]
となり、光子 1 個あたりの運動量を $\tilde{p}_{z}$ とすれば
\begin{equation}
\tilde{p}_{z}=\dfrac{p_{z}}{N}=\dfrac{\hbar\omega}{c}=\hbar k\label{eq:41}
\end{equation}
となる。ここで、角振動数 $\omega$ と波数 $k$ の関係 $\omega=ck$ を用いた。この運動量の方向は光(電磁波)の伝播方向を向いている。エネルギーの関係と合わせて式(\ref{eq:41})をベクトルの形で表せば
\[
E=\hbar\omega,\;\tilde{\boldsymbol{p}}=\hbar\boldsymbol{k}
\]
となる。この $\omega$ と $\boldsymbol{k}$ が 4 元ベクトルを形成することになる。
光子の角運動量は、式(\ref{eq:40})に示すように、左回り、右回り偏光に対応して $\pm\hbar$ の値しかもたない。これは光子が常に光速度で運動していて、光子が静止するような座標系を取ることができないことに関係している。光子が静止している座標系で見ると、$x,\,y,\,z$ 方向は全く同等なので、3 個の内部自由度がないと矛盾を生じるが、光子の場合は静止系がないので、運動に垂直な2次元の自由度だけが必要で、2 個の内部状態しかなくてもよいためである解釈できる [8]。
このことはまた、光子の静止系があるとすれば、その系では式(\ref{eq:2})における位相が一定となり、電場ベクトルは回転しないので角運動量が $S_{z}=0$ となり得るが、光子の静止系は存在しないため、$S_{z}=0$ となることは許されないと考えることもできる。
(注1)原子に対するトムソン模型によれば、原子内の電子の運動は単振動として記述される [9]。光との相互作用を考える場合は。原子内の電子の運動を単振動として考える場合が多い。
(注2)ここでの右回り、左回りの定義は、ファインマン物理学 [2] における定義とは逆になっている。
参考文献
3) 『電磁波の偏光』
4) 『右回り・左回り』